How To Use The Mean Value Theorem

Learning Objectives

• Explain the meaning of Rolle's theorem.
• Describe the significance of the Mean Value Theorem.
• State three important consequences of the Mean Value Theorem.

The Mean Value Theorem is one of the about important theorems in calculus. We expect at some of its implications at the end of this department. Starting time, let's start with a special case of the Mean Value Theorem, called Rolle's theorem.

Rolle'southward Theorem

Informally, Rolle'southward theorem states that if the outputs of a differentiable role [latex]f[/latex] are equal at the endpoints of an interval, then there must exist an interior point [latex]c[/latex] where [latex]f^{\prime number}(c)=0[/latex]. (Figure) illustrates this theorem.

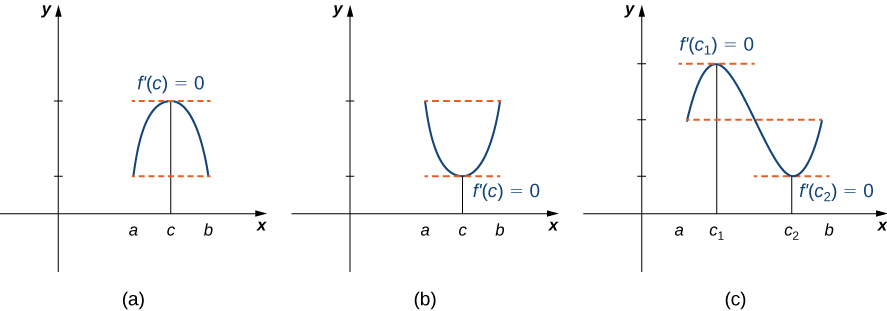
Figure one. If a differentiable function f satisfies [latex]f(a)=f(b)[/latex], so its derivative must be zilch at some indicate(due south) between [latex]a[/latex] and [latex]b[/latex].

Rolle's Theorem

Permit [latex]f[/latex] be a continuous function over the closed interval [latex][a,b][/latex] and differentiable over the open interval [latex](a,b)[/latex] such that [latex]f(a)=f(b)[/latex]. At that place and then exists at least i [latex]c \in (a,b)[/latex] such that [latex]f^{\prime}(c)=0[/latex].

Proof

Let [latex]k=f(a)=f(b)[/latex]. We consider three cases:

1. [latex]f(x)=chiliad[/latex] for all [latex]x \in (a,b)[/latex].
2. There exists [latex]x \in (a,b)[/latex] such that [latex]f(x)>1000[/latex].
3. There exists [latex]x \in (a,b)[/latex] such that [latex]f(x)<one thousand[/latex].

Example one: If [latex]f(10)=0[/latex] for all [latex]x \in (a,b)[/latex], then [latex]f^{\prime}(x)=0[/latex] for all [latex]10 \in (a,b)[/latex].

Case two: Since [latex]f[/latex] is a continuous part over the airtight, bounded interval [latex][a,b][/latex], past the farthermost value theorem, it has an absolute maximum. As well, since there is a point [latex]x \in (a,b)[/latex] such that [latex]f(ten)>k[/latex], the accented maximum is greater than [latex]g[/latex]. Therefore, the absolute maximum does not occur at either endpoint. As a consequence, the accented maximum must occur at an interior point [latex]c \in (a,b)[/latex]. Because [latex]f[/latex] has a maximum at an interior point [latex]c[/latex], and [latex]f[/latex] is differentiable at [latex]c[/latex], by Fermat'due south theorem, [latex]f^{\prime}(c)=0[/latex].

Instance iii: The example when there exists a signal [latex]x \in (a,b)[/latex] such that [latex]f(x)<k[/latex] is analogous to case 2, with maximum replaced by minimum.

□

An important point about Rolle'southward theorem is that the differentiability of the role [latex]f[/latex] is critical. If [latex]f[/latex] is not differentiable, even at a single betoken, the outcome may non concur. For case, the office [latex]f(x)=|x|-1[/latex] is continuous over [latex][-ane,one][/latex] and [latex]f(-i)=0=f(1)[/latex], but [latex]f^{\prime}(c) \ne 0[/latex] for any [latex]c \in (-one,1)[/latex] as shown in the following figure.

Figure two. Since [latex]f(x)=|x|-1[/latex] is non differentiable at [latex]x=0[/latex], the conditions of Rolle's theorem are not satisfied. In fact, the conclusion does non hold hither; there is no [latex]c \in (-1,one)[/latex] such that [latex]f^{\prime}(c)=0[/latex].

Permit'south at present consider functions that satisfy the conditions of Rolle's theorem and summate explicitly the points [latex]c[/latex] where [latex]f^{\prime}(c)=0[/latex].

Using Rolle'southward Theorem

For each of the post-obit functions, verify that the role satisfies the criteria stated in Rolle's theorem and find all values [latex]c[/latex] in the given interval where [latex]f^{\prime}(c)=0[/latex].

1. [latex]f(x)=x^2+2x[/latex] over [latex][-2,0][/latex]
2. [latex]f(x)=ten^three-4x[/latex] over [latex][-ii,two][/latex]

Verify that the office [latex]f(x)=2x^ii-8x+six[/latex] divers over the interval [latex][ane,3][/latex] satisfies the conditions of Rolle'due south theorem. Detect all points [latex]c[/latex] guaranteed by Rolle's theorem.

Show Solution

[latex]c=two[/latex]

The Hateful Value Theorem and Its Pregnant

Rolle's theorem is a special example of the Hateful Value Theorem. In Rolle'due south theorem, we consider differentiable functions [latex]f[/latex] that are aught at the endpoints. The Mean Value Theorem generalizes Rolle's theorem by considering functions that are non necessarily zero at the endpoints. Consequently, nosotros tin can view the Mean Value Theorem as a slanted version of Rolle'due south theorem ((Figure)). The Mean Value Theorem states that if [latex]f[/latex] is continuous over the airtight interval [latex][a,b][/latex] and differentiable over the open interval [latex](a,b)[/latex], then there exists a point [latex]c \in (a,b)[/latex] such that the tangent line to the graph of [latex]f[/latex] at [latex]c[/latex] is parallel to the secant line connecting [latex](a,f(a))[/latex] and [latex](b,f(b))[/latex].

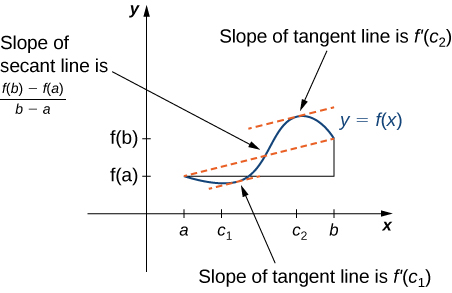
Figure 5. The Mean Value Theorem says that for a function that meets its atmospheric condition, at some point the tangent line has the same gradient as the secant line between the ends. For this function, there are 2 values [latex]c_1[/latex] and [latex]c_2[/latex] such that the tangent line to [latex]f[/latex] at [latex]c_1[/latex] and [latex]c_2[/latex] has the same slope as the secant line.

Hateful Value Theorem

Let [latex]f[/latex] be continuous over the airtight interval [latex][a,b][/latex] and differentiable over the open interval [latex](a,b)[/latex]. And so, there exists at least i signal [latex]c \in (a,b)[/latex] such that

[latex]f^{\prime}(c)=\frac{f(b)-f(a)}{b-a}[/latex].

Proof

The proof follows from Rolle'southward theorem by introducing an advisable part that satisfies the criteria of Rolle'south theorem. Consider the line connecting [latex](a,f(a))[/latex] and [latex](b,f(b))[/latex]. Since the slope of that line is

[latex]\frac{f(b)-f(a)}{b-a}[/latex]

and the line passes through the point [latex](a,f(a))[/latex], the equation of that line can exist written as

[latex]y=\frac{f(b)-f(a)}{b-a}(10-a)+f(a)[/latex].

Let [latex]thousand(x)[/latex] denote the vertical divergence between the point [latex](x,f(x))[/latex] and the point [latex](x,y)[/latex] on that line. Therefore,

[latex]yard(x)=f(ten)-[\frac{f(b)-f(a)}{b-a}(x-a)+f(a)][/latex].

Figure half dozen. The value [latex]g(x)[/latex] is the vertical deviation betwixt the point [latex](x,f(x))[/latex] and the point [latex](x,y)[/latex] on the secant line connecting [latex](a,f(a))[/latex] and [latex](b,f(b)).[/latex]

Since the graph of [latex]f[/latex] intersects the secant line when [latex]x=a[/latex] and [latex]ten=b[/latex], we meet that [latex]g(a)=0=m(b)[/latex]. Since [latex]f[/latex] is a differentiable office over [latex](a,b)[/latex], [latex]chiliad[/latex] is likewise a differentiable function over [latex](a,b)[/latex]. Furthermore, since [latex]f[/latex] is continuous over [latex][a,b][/latex], [latex]g[/latex] is too continuous over [latex][a,b][/latex]. Therefore, [latex]g[/latex] satisfies the criteria of Rolle'southward theorem. Consequently, there exists a signal [latex]c \in (a,b)[/latex] such that [latex]yard^{\prime}(c)=0[/latex]. Since

[latex]g^{\prime number}(ten)=f^{\prime}(10)-\frac{f(b)-f(a)}{b-a}[/latex],

we see that

[latex]grand^{\prime}(c)=f^{\prime}(c)-\frac{f(b)-f(a)}{b-a}[/latex].

Since [latex]m^{\prime}(c)=0[/latex], nosotros conclude that

[latex]f^{\prime number}(c)=\frac{f(b)-f(a)}{b-a}[/latex].

□

In the adjacent example, nosotros show how the Hateful Value Theorem tin be applied to the office [latex]f(x)=\sqrt{x}[/latex] over the interval [latex][0,nine][/latex]. The method is the aforementioned for other functions, although sometimes with more than interesting consequences.

Verifying that the Mean Value Theorem Applies

For [latex]f(x)=\sqrt{ten}[/latex] over the interval [latex][0,ix][/latex], show that [latex]f[/latex] satisfies the hypothesis of the Mean Value Theorem, and therefore there exists at to the lowest degree ane value [latex]c \in (0,ix)[/latex] such that [latex]f^{\prime}(c)[/latex] is equal to the slope of the line connecting [latex](0,f(0))[/latex] and [latex](nine,f(ix))[/latex]. Find these values [latex]c[/latex] guaranteed by the Hateful Value Theorem.

I awarding that helps illustrate the Mean Value Theorem involves velocity. For example, suppose we bulldoze a car for 1 hr down a directly road with an average velocity of 45 mph. Let [latex]s(t)[/latex] and [latex]5(t)[/latex] denote the position and velocity of the car, respectively, for [latex]0 \le t \le 1[/latex] hour. Assuming that the position function [latex]s(t)[/latex] is differentiable, nosotros can apply the Hateful Value Theorem to conclude that, at some time [latex]c \in (0,one)[/latex], the speed of the car was exactly

[latex]v(c)=due south^{\prime}(c)=\frac{southward(1)-s(0)}{1-0}=45[/latex] mph.

Hateful Value Theorem and Velocity

If a rock is dropped from a summit of 100 ft, its position [latex]t[/latex] seconds afterwards it is dropped until it hits the ground is given by the function [latex]s(t)=-16t^2+100[/latex].

1. Determine how long information technology takes before the rock hits the ground.
2. Find the average velocity [latex]v_{\text{avg}}[/latex] of the rock for when the rock is released and the stone hits the ground.
3. Detect the fourth dimension [latex]t[/latex] guaranteed by the Hateful Value Theorem when the instantaneous velocity of the rock is [latex]v_{\text{avg}}[/latex].

Suppose a ball is dropped from a height of 200 ft. Its position at fourth dimension [latex]t[/latex] is [latex]s(t)=-16t^two+200[/latex]. Find the fourth dimension [latex]t[/latex] when the instantaneous velocity of the ball equals its boilerplate velocity.

Show Solution

[latex]\frac{5}{2\sqrt{two}}[/latex] sec

Corollaries of the Mean Value Theorem

Let'due south now await at 3 corollaries of the Mean Value Theorem. These results take of import consequences, which we employ in upcoming sections.

At this bespeak, nosotros know the derivative of any constant function is cipher. The Hateful Value Theorem allows us to conclude that the antipodal is too truthful. In particular, if [latex]f^{\prime}(x)=0[/latex] for all [latex]ten[/latex] in some interval [latex]I[/latex], and so [latex]f(ten)[/latex] is constant over that interval. This result may seem intuitively obvious, but it has important implications that are not obvious, and we discuss them shortly.

Corollary 1: Functions with a Derivative of Zero

Allow [latex]f[/latex] be differentiable over an interval [latex]I[/latex]. If [latex]f^{\prime number}(x)=0[/latex] for all [latex]x \in I[/latex], then [latex]f(10)[/latex] is constant for all [latex]x \in I[/latex].

Proof

Since [latex]f[/latex] is differentiable over [latex]I[/latex], [latex]f[/latex] must be continuous over [latex]I[/latex]. Suppose [latex]f(ten)[/latex] is not constant for all [latex]x[/latex] in [latex]I[/latex]. So there be [latex]a,b \in I[/latex], where [latex]a \ne b[/latex] and [latex]f(a) \ne f(b)[/latex]. Cull the notation then that [latex]a<b[/latex]. Therefore,

[latex]\frac{f(b)-f(a)}{b-a} \ne 0[/latex].

Since [latex]f[/latex] is a differentiable function, by the Hateful Value Theorem, there exists [latex]c \in (a,b)[/latex] such that

[latex]f^{\prime}(c)=\frac{f(b)-f(a)}{b-a}[/latex].

Therefore, there exists [latex]c \in I[/latex] such that [latex]f^{\prime number}(c) \ne 0[/latex], which contradicts the assumption that [latex]f^{\prime number}(x)=0[/latex] for all [latex]10 \in I[/latex].

□

From (Effigy), information technology follows that if two functions take the aforementioned derivative, they differ by, at near, a constant.

Corollary 2: Constant Difference Theorem

If [latex]f[/latex] and [latex]thou[/latex] are differentiable over an interval [latex]I[/latex] and [latex]f^{\prime}(x)=g^{\prime number}(10)[/latex] for all [latex]10 \in I[/latex], then [latex]f(x)=g(x)+C[/latex] for some constant [latex]C[/latex].

Proof

Let [latex]h(x)=f(x)-thou(x)[/latex]. Then, [latex]h^{\prime}(x)=f^{\prime}(x)-1000^{\prime}(x)=0[/latex] for all [latex]x \in I[/latex]. Past Corollary 1, there is a abiding [latex]C[/latex] such that [latex]h(x)=C[/latex] for all [latex]x \in I[/latex]. Therefore, [latex]f(x)=yard(x)+C[/latex] for all [latex]x \in I[/latex].

□

The third corollary of the Mean Value Theorem discusses when a role is increasing and when it is decreasing. Call up that a part [latex]f[/latex] is increasing over [latex]I[/latex] if [latex]f(x_1)<f(x_2)[/latex] whenever [latex]x_1<x_2[/latex], whereas [latex]f[/latex] is decreasing over [latex]I[/latex] if [latex]f(x_1)>f(x_2)[/latex] whenever [latex]x_1<x_2[/latex]. Using the Mean Value Theorem, we can show that if the derivative of a function is positive, so the function is increasing; if the derivative is negative, and so the function is decreasing ((Figure)). We make use of this fact in the adjacent section, where nosotros testify how to use the derivative of a function to locate local maximum and minimum values of the function, and how to decide the shape of the graph.

This fact is important because it means that for a given part [latex]f[/latex], if at that place exists a office [latex]F[/latex] such that [latex]F^{\prime number}(x)=f(ten)[/latex]; then, the just other functions that have a derivative equal to [latex]f[/latex] are [latex]F(ten)+C[/latex] for some constant [latex]C[/latex]. We hash out this consequence in more detail later in the chapter.

Effigy 9. If a function has a positive derivative over some interval [latex]I[/latex], then the function increases over that interval [latex]I[/latex]; if the derivative is negative over some interval [latex]I[/latex], then the office decreases over that interval [latex]I[/latex].

Corollary 3: Increasing and Decreasing Functions

Let [latex]f[/latex] be continuous over the closed interval [latex][a,b][/latex] and differentiable over the open interval [latex](a,b)[/latex].

1. If [latex]f^{\prime number}(x)>0[/latex] for all [latex]x \in (a,b)[/latex], and then [latex]f[/latex] is an increasing function over [latex][a,b][/latex].
2. If [latex]f^{\prime}(x)<0[/latex] for all [latex]x \in (a,b)[/latex], then [latex]f[/latex] is a decreasing function over [latex][a,b][/latex].

Proof

Nosotros will prove 1.; the proof of two. is similar. Suppose [latex]f[/latex] is non an increasing part on [latex]I[/latex]. And then in that location exist [latex]a[/latex] and [latex]b[/latex] in [latex]I[/latex] such that [latex]a<b[/latex], but [latex]f(a) \ge f(b)[/latex]. Since [latex]f[/latex] is a differentiable function over [latex]I[/latex], by the Hateful Value Theorem there exists [latex]c \in (a,b)[/latex] such that

[latex]f^{\prime}(c)=\frac{f(b)-f(a)}{b-a}[/latex].

Since [latex]f(a) \ge f(b)[/latex], we know that [latex]f(b)-f(a) \le 0[/latex]. Also, [latex]a<b[/latex] tells the states that [latex]b-a>0[/latex]. We conclude that

[latex]f^{\prime}(c)=\frac{f(b)-f(a)}{b-a} \le 0[/latex].

Yet, [latex]f^{\prime}(10)>0[/latex] for all [latex]10 \in I[/latex]. This is a contradiction, and therefore [latex]f[/latex] must be an increasing office over [latex]I[/latex].

□

Primal Concepts

• If [latex]f[/latex] is continuous over [latex][a,b][/latex] and differentiable over [latex](a,b)[/latex] and [latex]f(a)=0=f(b)[/latex], so in that location exists a point [latex]c \in (a,b)[/latex] such that [latex]f^{\prime}(c)=0[/latex]. This is Rolle's theorem.
• If [latex]f[/latex] is continuous over [latex][a,b][/latex] and differentiable over [latex](a,b)[/latex], then in that location exists a indicate [latex]c \in (a,b)[/latex] such that

  [latex]f^{\prime}(c)=\frac{f(b)-f(a)}{b-a}[/latex].

  This is the Mean Value Theorem.

• If [latex]f^{\prime number}(10)=0[/latex] over an interval [latex]I[/latex], and so [latex]f[/latex] is abiding over [latex]I[/latex].
• If ii differentiable functions [latex]f[/latex] and [latex]k[/latex] satisfy [latex]f^{\prime number}(x)=one thousand^{\prime}(x)[/latex] over [latex]I[/latex], and then [latex]f(x)=g(10)+C[/latex] for some constant [latex]C[/latex].
• If [latex]f^{\prime}(10)>0[/latex] over an interval [latex]I[/latex], then [latex]f[/latex] is increasing over [latex]I[/latex]. If [latex]f^{\prime}(x)<0[/latex] over [latex]I[/latex], then [latex]f[/latex] is decreasing over [latex]I[/latex].

1. Why do yous need continuity to apply the Hateful Value Theorem? Construct a counterexample.

2. Why do you lot need differentiability to apply the Mean Value Theorem? Find a counterexample.

Evidence Solution

One example is [latex]f(x)=|x|+3, \, -2 \le x \le two[/latex]

3. When are Rolle'southward theorem and the Mean Value Theorem equivalent?

iv. If you have a office with a discontinuity, is it still possible to accept [latex]f^{\prime}(c)(b-a)=f(b)-f(a)[/latex]? Draw such an example or testify why not.

Show Solution

Yes, but the Mean Value Theorem still does not apply

For the following exercises, determine over what intervals (if whatever) the Mean Value Theorem applies. Justify your respond.

v. [latex]y= \sin (\pi x)[/latex]

6. [latex]y=\frac{i}{x^iii}[/latex]

Show Solution

[latex](−\infty,0), \, (0,\infty)[/latex]

7. [latex]y=\sqrt{4-x^two}[/latex]

8. [latex]y=\sqrt{x^2-four}[/latex]

Bear witness Solution

[latex](−\infty,-two), \, (2,\infty)[/latex]

9. [latex]y=\ln (3x-5)[/latex]

For the post-obit exercises, graph the functions on a calculator and draw the secant line that connects the endpoints. Approximate the number of points [latex]c[/latex] such that [latex]f^{\prime}(c)(b-a)=f(b)-f(a)[/latex].

x. [T] [latex]y=3x^iii+2x+1[/latex] over [latex][-1,1][/latex]

eleven. [T] [latex]y= \tan (\frac{\pi}{four}x)[/latex] over [latex][-\frac{3}{two},\frac{3}{2}][/latex]

12. [T] [latex]y=10^ii \cos (\pi x)[/latex] over [latex][-2,2][/latex]

13. [T] [latex]y=x^6-\frac{3}{4}ten^v-\frac{9}{8}x^4+\frac{15}{16}x^3+\frac{three}{32}ten^2+\frac{iii}{16}x+\frac{1}{32}[/latex] over [latex][-1,1][/latex]

For the following exercises, apply the Mean Value Theorem and find all points [latex]0<c<2[/latex] such that [latex]f(2)-f(0)=f^{\prime}(c)(2-0)[/latex].

xiv. [latex]f(x)=x^3[/latex]

Show Solution

[latex]c=\frac{2\sqrt{3}}{3}[/latex]

15. [latex]f(x)= \sin (\pi x)[/latex]

16. [latex]f(x)= \cos (ii\pi x)[/latex]

Prove Solution

[latex]c=\frac{one}{2}, \, 1, \, \frac{3}{2}[/latex]

17. [latex]f(x)=1+10+x^ii[/latex]

18. [latex]f(10)=(x-i)^{10}[/latex]

Show Solution

[latex]c=one[/latex]

19. [latex]f(x)=(x-1)^9[/latex]

For the following exercises, testify there is no [latex]c[/latex] such that [latex]f(1)-f(-1)=f^{\prime}(c)(2)[/latex]. Explain why the Mean Value Theorem does non utilize over the interval [latex][-1,1][/latex]

20. [latex]f(x)=|x-\frac{i}{2}|[/latex]

Show Solution

Not differentiable

21. [latex]f(x)=\frac{1}{x^ii}[/latex]

22. [latex]f(ten)=\sqrt{|x|}[/latex]

Show Solution

Not differentiable

23. [latex]f(10)=⌊10⌋[/latex] (Hint: This is chosen the floor function and information technology is defined and then that [latex]f(x)[/latex] is the largest integer less than or equal to [latex]x[/latex].)

For the following exercises, determine whether the Mean Value Theorem applies for the functions over the given interval [latex][a,b][/latex]. Justify your answer.

24. [latex]y=east^10[/latex] over [latex][0,1][/latex]

25. [latex]y=\ln (2x+3)[/latex] over [latex][-\frac{3}{2},0][/latex]

26. [latex]f(x)= \tan (2\pi 10)[/latex] over [latex][0,2][/latex]

Show Solution

The Mean Value Theorem does not apply since the function is discontinuous at [latex]x=\frac{1}{4}, \, \frac{3}{4}, \, \frac{5}{4}, \, \frac{7}{4}[/latex].

27. [latex]y=\sqrt{nine-x^2}[/latex] over [latex][-3,3][/latex]

28. [latex]y=\frac{i}{|x+one|}[/latex] over [latex][0,3][/latex]

29. [latex]y=x^iii+2x+one[/latex] over [latex][0,6][/latex]

30. [latex]y=\frac{ten^2+3x+2}{x}[/latex] over [latex][-1,one][/latex]

Show Solution

The Mean Value Theorem does not apply; discontinuous at [latex]x=0[/latex].

31. [latex]y=\frac{ten}{ \sin (\pi x)+1}[/latex] over [latex][0,ane][/latex]

32. [latex]y=\ln (ten+1)[/latex] over [latex][0,east-1][/latex]

33. [latex]y=x \sin (\pi x)[/latex] over [latex][0,2][/latex]

34. [latex]y=5+|x|[/latex] over [latex][-1,i][/latex]

Bear witness Solution

The Hateful Value Theorem does not apply; not differentiable at [latex]ten=0[/latex].

For the following exercises, consider the roots of the equation.

35. Show that the equation [latex]y=x^3+3x^2+16[/latex] has exactly 1 real root. What is it?

36. Find the conditions for exactly one root (double root) for the equation [latex]y=x^2+bx+c[/latex]

Show Solution

[latex]b=\pm ii\sqrt{c}[/latex]

37. Find the conditions for [latex]y=east^x-b[/latex] to have one root. Is it possible to accept more than one root?

For the post-obit exercises, use a calculator to graph the role over the interval [latex][a,b][/latex] and graph the secant line from [latex]a[/latex] to [latex]b[/latex]. Employ the calculator to gauge all values of [latex]c[/latex] as guaranteed by the Mean Value Theorem. And then, detect the exact value of [latex]c[/latex], if possible, or write the terminal equation and apply a figurer to estimate to four digits.

38. [T] [latex]y= \tan (\pi x)[/latex] over [latex][-\frac{one}{iv},\frac{1}{4}][/latex]

Show Solution

[latex]c=\pm \frac{one}{\pi} \cos^{-1}(\frac{\sqrt{\pi}}{2})[/latex]; [latex]c=\pm 0.1533[/latex]

39. [T] [latex]y=\frac{i}{\sqrt{ten+1}}[/latex] over [latex][0,3][/latex]

40. [T] [latex]y=|ten^2+2x-4|[/latex] over [latex][-4,0][/latex]

Testify Solution

The Hateful Value Theorem does not use.

41. [T] [latex]y=x+\frac{1}{ten}[/latex] over [latex][\frac{ane}{two},4][/latex]

42. [T] [latex]y=\sqrt{x+1}+\frac{i}{x^2}[/latex] over [latex][3,viii][/latex]

Testify Solution

[latex]\frac{1}{ii\sqrt{c+ane}}-\frac{2}{c^3}=\frac{521}{2880}[/latex]; [latex]c=3.133,5.867[/latex]

43. At 10:17 a.m., yous laissez passer a police car at 55 mph that is stopped on the freeway. You lot pass a second police automobile at 55 mph at 10:53 a.m., which is located 39 mi from the starting time police car. If the speed limit is threescore mph, can the constabulary cite you for speeding?

44. Two cars drive from ane spotlight to the next, leaving at the same time and arriving at the same fourth dimension. Is in that location always a fourth dimension when they are going the same speed? Testify or disprove.

45. Show that [latex]y= \sec^2 ten[/latex] and [latex]y= \tan^2 x[/latex] have the aforementioned derivative. What can y'all say about [latex]y= \sec^2 x - \tan^2 x[/latex]?

46. Show that [latex]y= \csc^ii x[/latex] and [latex]y= \cot^2 x[/latex] have the aforementioned derivative. What can you say virtually [latex]y= \csc^two x - \cot^ii x[/latex]?

Show Solution

It is constant.

Glossary

mean value theorem

if [latex]f[/latex] is continuous over [latex][a,b][/latex] and differentiable over [latex](a,b)[/latex], so there exists [latex]c \in (a,b)[/latex] such that

[latex]f^{\prime}(c)=\frac{f(b)-f(a)}{b-a}[/latex]

rolle'south theorem

if [latex]f[/latex] is continuous over [latex][a,b][/latex] and differentiable over [latex](a,b)[/latex], and if [latex]f(a)=f(b)[/latex], then in that location exists [latex]c \in (a,b)[/latex] such that [latex]f^{\prime}(c)=0[/latex]

How To Use The Mean Value Theorem,

Source: https://courses.lumenlearning.com/suny-openstax-calculus1/chapter/the-mean-value-theorem/

Posted by: sandersdideseld43.blogspot.com

Share this post